Machine Learning: Classification

• 基于CIFAR-10图像分类任务训练线性分类器、MLP和CNN模型
  • 一、模型原理
    • 1）Softmax分类器
    • 2）MLP
    • 3）CNN
    • 4）网络参数
      • 1、CUDA加速
      • 2、损失函数
      • 3、优化器
        • SGD（Stochastic Gradient Descent）
        • SGD Momentum
        • Adam
  • 二、代码框架
    • 1）数据读取及预处理
    • 2）单次训练
    • 3）评估正确率
    • 4）main
  • 三、实验分析
    • 1）Softmax线性模型
    • 2）MLP模型
    • 3）CNN模型
      • 1、对优化算法及其参数的实验
      • 2、对网络结构的实验
    • 4）对比三个模型在CIFAR-10图像分类任务上的性能

基于CIFAR-10图像分类任务训练线性分类器、MLP和CNN模型

一、模型原理

1）Softmax分类器

Softmax分类器是一个单层线性神经网络，即只有一个输入层、一个输出层，再经过Softmax函数激活层，得到标签的预测概率。Softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质。

实现一个Softmax线性分类模型：

class Softmax(nn.Module):
    def __init__(self, inNum, outNum) -> None:
        super(Softmax, self).__init__()
        self.out = nn.Linear(inNum,outNum)
    def forward(self, x):
        y = F.relu(self.out(x.view(x.shape[0],-1)))
        y = F.log_softmax(y,dim=0)
        return y 

2）MLP

通过在网络中加入一个或多个隐藏层，可以克服线性模型的限制， 使其能处理更普遍的、非单调的函数关系类型。将许多全连接层堆叠在一起，每一层都输出到上面的层，直到生成最后的输出。 我们可以把前L−1层看作表示，把最后一层看作线性预测器。 这种架构通常称为多层感知机（multilayer perceptron），通常缩写为MLP。

实现一个MLP模型：

该神经网络结构由一个输入层、三个隐藏层及一个输出层构成，在层与层之间使用ReLU激活层，最后用Softmax计算标签的预测概率。

class MLP(nn.Module): 
    def __init__(self, inNum, outNum, hidden,hid2,hid3) -> None:
        super(MLP, self).__init__()
        self.hid = nn.Linear(inNum,hidden)
        self.hid2 = nn.Linear(hidden,hid2)
        self.hid3 = nn.Linear(hid2,hid3)
        self.out = nn.Linear(hid3,outNum)
        
    def forward(self, x):
        x = F.relu(self.hid(x.view(x.shape[0],-1))) #input(3,32,32) output(1024)
        x = F.relu(self.hid2(x.view(x.shape[0],-1)))#output(256)
        x = F.relu(self.hid3(x.view(x.shape[0],-1)))#output(84)
        x = F.relu(self.out(x.view(x.shape[0],-1)))#output(10)
        x = F.log_softmax(x,dim=0)
        return x

3）CNN

卷积神经网络（convolutional neural network，CNN）是一类强大的、为处理图像数据而设计的神经网络。使用前述的模型时，将图像数据展平成一维向量而忽略了每个图像的空间结构信息，卷积神经网络则能弥补这个缺漏。

LeNet（LeNet-5）由两个部分组成：

• 卷积编码器：由两个卷积层组成;
• 全连接层密集块：由三个全连接层组成。

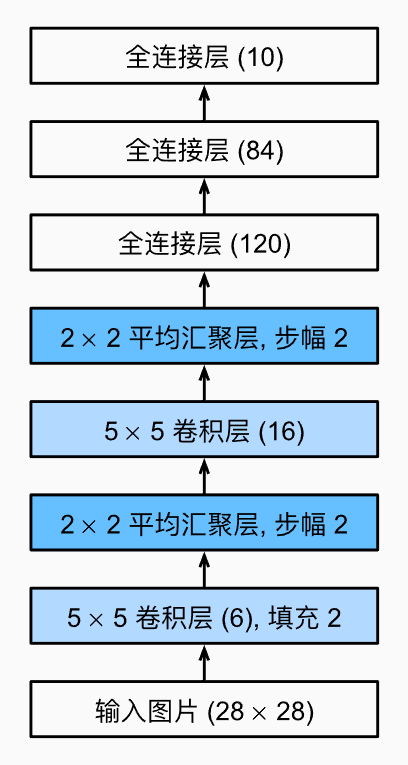
实现一个LeNet模型：

class LeNet(nn.Module):
    def __init__(self):
        super(LeNet,self).__init__()
        self.conv1 = nn.Conv2d(3,16,5)
        self.pool1 = nn.MaxPool2d(2,2)
        self.conv2 = nn.Conv2d(16,32,5)
        self.pool2 = nn.MaxPool2d(2,2)
        self.fc1 = nn.Linear(32*5*5,120)
        self.fc2 = nn.Linear(120,84)
        self.fc3 = nn.Linear(84,10)
        

    def forward(self, x):
        x = F.relu(self.conv1(x))#input(3,32,32) output(16,28,28)
        x = self.pool1(x) #output(16，14，14)
        x = F.relu(self.conv2(x)) #output(32,10,10)
        x = self.pool2(x) #output(32,5,5)
        x = x.view(-1,32*5*5) #output(5*5*32)
        x = F.relu(self.fc1(x)) #output(120)
        x = F.relu(self.fc2(x)) #output(84)
        x = F.relu(self.fc3(x))  # output(10)
        x = F.log_softmax(x, dim=1)
        return x

4）网络参数

1、CUDA加速

利用GPU进行计算、让CPU读取数据，可以大幅减少训练的耗时，为此需要将数据与网络迁移到GPU上进行大规模计算。

import torch
from torch import nn

# 查看gpu信息
cudaMsg = torch.cuda.is_available()
gpuCount = torch.cuda.device_count()
print("1.是否存在GPU:{}".format(cudaMsg), "如果存在有：{}个".format(gpuCount))

# 将数据/网络移到GPU上
net = net.cuda()

# 命令行
$ nvidia-smi #可以查看当前GPU适配的CUDA版本及显卡占用率
NVIDIA-SMI 522.25       Driver Version: 522.25       CUDA Version: 11.8


$ nvcc -V #可以确认CUDA是否已安装成功

nvcc: NVIDIA (R) Cuda compiler driver
Copyright (c) 2005-2022 NVIDIA Corporation
Built on Wed_Sep_21_10:41:10_Pacific_Daylight_Time_2022
Cuda compilation tools, release 11.8, V11.8.89
Build cuda_11.8.r11.8/compiler.31833905_0

事实上对于该模型，BatchSize=500时，N卡占用率顶多70%，多数时间有大量空余，真正占用时间的是迭代数据时，CPU对数据集图像的读取及预处理（即transform操作），这是由于CPU对Tensor的处理很慢，而torchvision库没有将数据集迁移到GPU进行预处理计算的API，若要解决这个问题，只能使用DALI或其余库接口加速预处理与数据读取，或者将预处理后的数据集进行保存。

2、损失函数

由于是预测标签概率类型的网络，在此次实验中都采用交叉熵函数。

import torch.nn as nn
# 损失函数
loss = nn.CrossEntropyLoss()

3、优化器

import torch

# SGD / SGD Momentum
optimizer = torch.optim.SGD(net.parameters(),lr=0.03,momentum=0.9, weight_decay=1e-5) 
# Adam
optimizer = torch.optim.Adam(net.parameters(),weight_decay=1e-5) 

# 控制学习率指数衰减
torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.98)
# 控制学习率按固定步长衰减
torch.optim.lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.65)

SGD（Stochastic Gradient Descent）

随机梯度下降算法即是在给定数据集中，每次随机选择一则数据，根据该数据的训练结果计算损失梯度，更新参数。

SGD Momentum

在随机梯度的学习算法中，每一步的步幅都是固定的，而在动量学习算法中，每一步走多远不仅依赖于本次的梯度的大小，还取决于过去的速度。速度v是累积各轮训练参数的梯度，速度越大，依赖以前的梯度越大。物理学中，用变量v表示速度，表明参数在参数空间移动的方向即速率，而代价函数的负梯度表示参数在参数空间移动的力，根据牛顿定律，动量等于质量乘以速度，而在动量学习算法中，我们假设质量的单位为1，因此速度v就可以直接当做动量了，我们同时引入超参数$\beta$，其取值在$[0,1]$范围之间，用于调节先前梯度（力）的衰减效果。

Adam

自适应动量优化算法结合了RMSProp和动量学习法的优势。

二、代码框架

1）数据读取及预处理

直接调用torchvision.datasets中的CIFAR10数据集，对图像进行随机翻转、随机灰度调正、转换为Tensor张量、正则化等预处理操作，返回torch.utils.data.DataLoader作为迭代器。

import torch
import torchvision
import torchvision.transforms as transforms


batch = 500 # batch_size

def load_data(): # 读取数据，返回迭代器
    mean = torch.tensor([0.4915, 0.4823, 0.4468])   
    std = torch.tensor([0.2470, 0.2435, 0.2616])
    # 图像预处理操作
    transform = transforms.Compose(
        [
            transforms.RandomHorizontalFlip(),
            transforms.RandomGrayscale(),
            transforms.ToTensor(),
            transforms.Normalize(mean,std)])

    transform1 = transforms.Compose(
        [
            transforms.ToTensor(),
            transforms.Normalize(mean,std)])

    
    trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
                                                download=False, transform=transform)
    trainloader = torch.utils.data.DataLoader(trainset, batch_size=batch,
                                                shuffle=True)#,num_workers=1,pin_memory=True)

    testset = torchvision.datasets.CIFAR10(root='./data', train=False,
                                                download=False, transform=transform1)
    testloader = torch.utils.data.DataLoader(testset, batch_size=batch,
                                                shuffle=False)#,num_workers=1,pin_memory=True)
    
    return trainloader,testloader

2）单次训练

实现一个epoch内的训练函数：

1. 向前传播得到预测标签
2. 根据预测值计算损失值
3. 根据损失值进行反向传播，得到各参数的梯度
4. 根据梯度下降更新参数
5. 返回损失值

def SingleTrain(net,train_iter,loss,optim):
    """train for one epoch

    Args:
        net (nn.module): training model
        train_iter (dataloader): iterator of training set
        loss (): loss function of the model
        optim (): optimizer of the model

    Returns:
        float: loss value
    """
        net.train() # 开启训练模式
        # 将计算累计loss值的变量定义在GPU上，无需在计算时在CPU与GPU之间移动，耗费时间
        los = torch.zeros(1).cuda()
        for k,data in enumerate(train_iter,0):
            x,y = data
            # 将数据迁移到GPU
            x = x.cuda()
            y = y.cuda()
            # 清零梯度
            optim.zero_grad()
            # 向前传播，输出预测标签
            haty = net(x)
            # 计算损失值
            l = loss(haty,y)
            # 反向传播，计算得到每个参数的梯度值
            l.backward()
            # 梯度下降，由优化器更新参数
            optim.step()
            # 累计损失值
            los += (los * k + l.detach()) / (k + 1)
            #right += torch.eq(torch.max(haty, dim=1)[1], y).sum()
        return los.item()

3）评估正确率

计算用当前网络预测正确的样本个数。

@torch.no_grad() # 使新增的tensor没有梯度，使带梯度的tensor能够进行原地运算
def score(net,data_iter):
    net.eval() # 开启评估模式
    # 将计算累计正确预测样例数的变量定义在GPU上，无需在计算时在CPU与GPU之间移动，耗费时间
    right_sum = torch.zeros(1).cuda()
    for k,data in enumerate(data_iter):
        X,y = data
        X = X.cuda()
        y = y.cuda()
        # 计算预测标签一致的样例数
        right_sum += torch.eq(torch.max(net(X), dim=1)[1], y).sum()
    return right_sum.item()

4）main

def main():
    input,output = 3072,10
    hid,hid2,hid3 = 1024,256,84
    trainlen,testlen = 50000,10000
    train_iter, test_iter = load_data()
    #net = LeNet()
    #net = MLP(input,output,hid,hid2,hid3)
    #net = Softmax(input,output)
    net = CNN()
    net = net.cuda()
    #损失函数
    loss = nn.CrossEntropyLoss()
    #优化函数
    optimizer = torch.optim.SGD(net.parameters(),lr=0.03,momentum=0.9, weight_decay=1e-5) 
    torch.optim.lr_scheduler.ExponentialLR(optimizer, gamma=0.98)
    # torch.optim.lr_scheduler.StepLR(optimizer, step_size=10, gamma=0.65)
    #optimizer = torch.optim.Adam(net.parameters(),weight_decay=1e-5) 
    epoch = 40
    start = time()
    for i in range(epoch):
        t = time()
        loss_visual.append(SingleTrain(net,train_iter,loss,optimizer))
        # train.append(score(net,train_iter)/trainlen)
        test.append(score(net,test_iter)/testlen)
        print(f'epoch: {i}\nloss:{loss_visual[-1]}\ntest accuracy:{test[-1]}')
        print(f'Time for this epoch: {time()-t}s')
    
    print(f'Time: {time()-start}s\n for {epoch} epoches.\nAverage {(time()-start)/epoch} for each.')
    print(f'The optimal test accuracy:{max(test)}')
    plt.plot(range(len(loss_visual)),loss_visual)
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    
    plt.figure()
    #plt.plot(range(len(train)),train,color='blue', label='Train Accuracy')
    plt.plot(range(len(test)),test,color='purple', label='Test Accuracy')
    plt.legend() # 显示图例
    plt.xlabel('Epoch')
    plt.ylabel('Accuracy')
    plt.ylim((0,1))
    
    
    plt.show()

if __name__ == '__main__':
    main()

三、实验分析

1）Softmax线性模型

对更改优化算法、学习率lr及迭代次数epoch等参数进行实验。

运行结果：

优化器及参数	损失值	训练集表现	测试集表现
Adam lr=0.002 epoch=300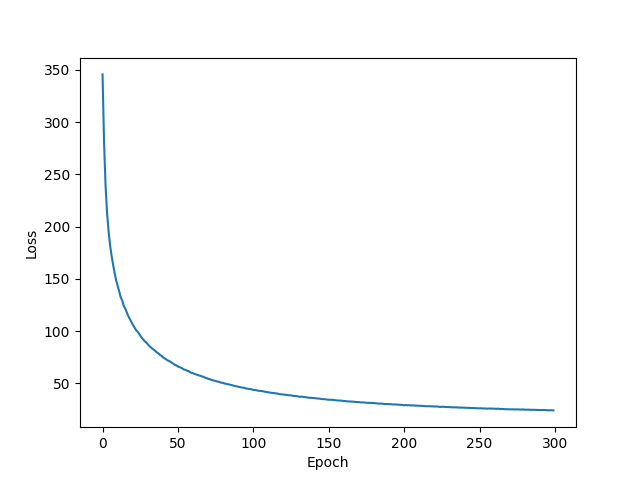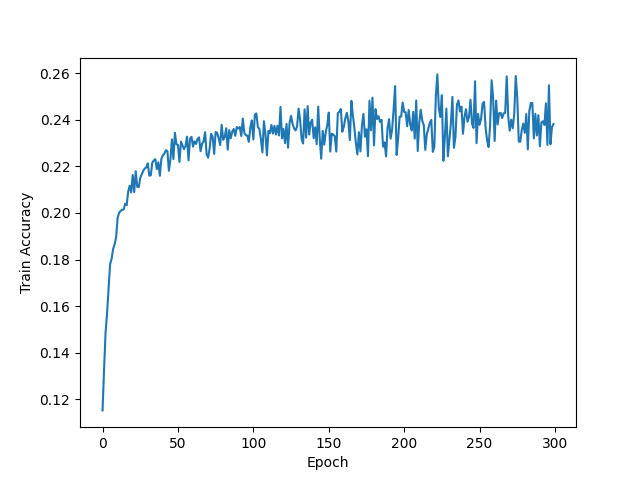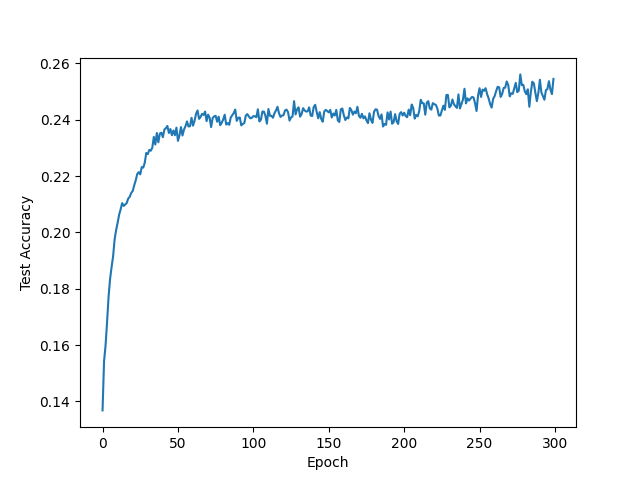
Adam lr=0.05 epoch=30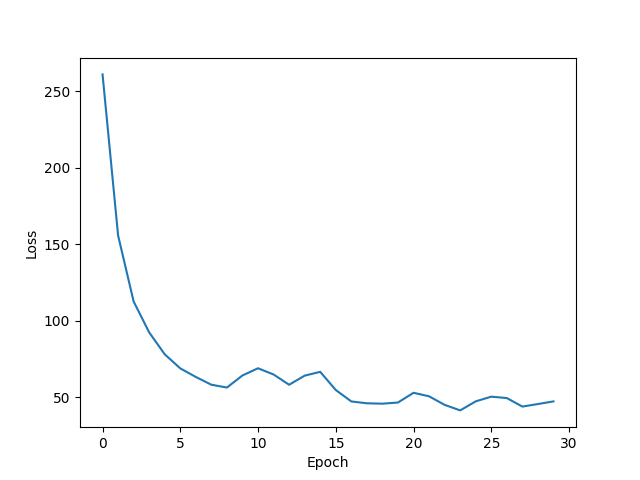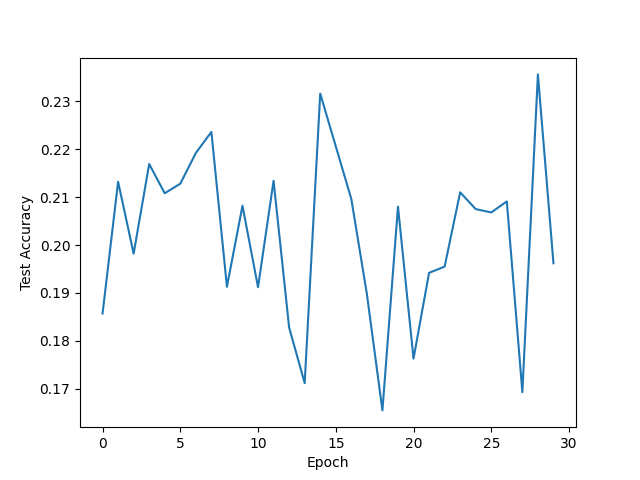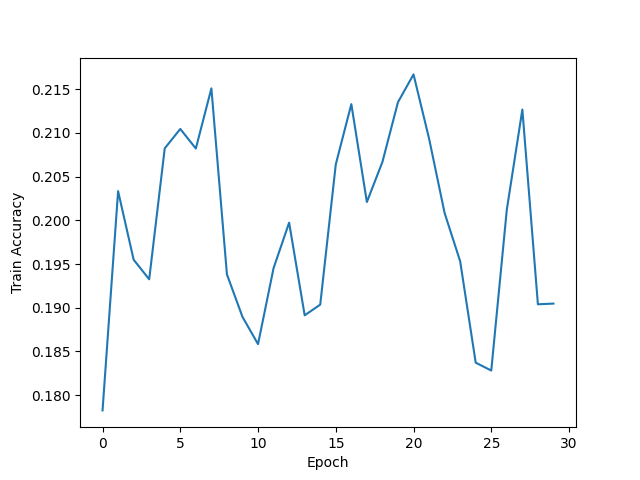
SGD lr=0.03 momentum=0.9 weight_decay=1e-5 epoch=40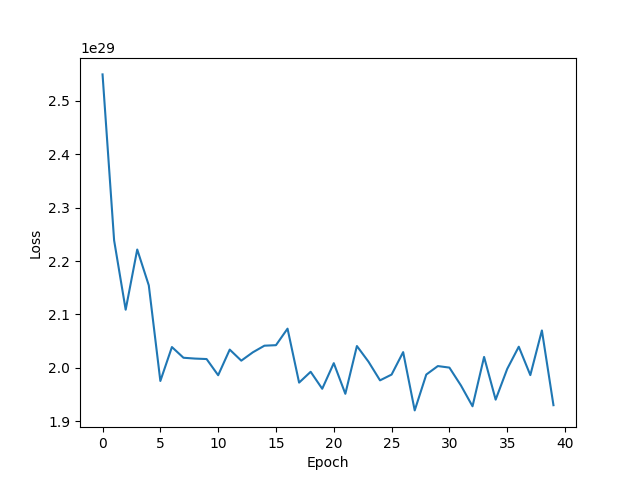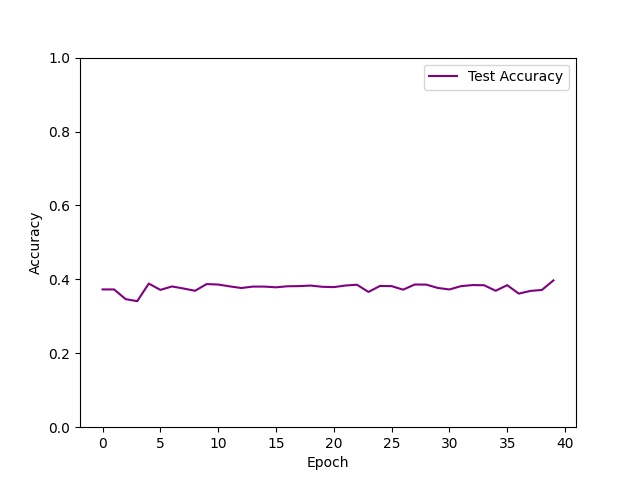

从表中可以看出：

1. 在训练效率上，使用不同优化算法的时间是相近的，Adam优化算法会较快。Adam采用自适应优化，所以它的优势是训练快，但是问题在于更容易陷入局部最优、鞍点。
2. 在训练效果上：
   1. 使用Adam优化算法时，正确率不如使用SGD Momentum优化算法，损失函数正常收敛，学习率较大时损失函数出现微小的震荡。当学习率为0.002时，迭代了300次后，训练集正确率仅仅是从12%增加到约26%，测试集也是，说明欠拟合。当学习率为0.05时，迭代了30次后，训练集与测试集正确率都在17%到23%左右震荡，绘制正确率图像时没有将y轴范围设置在[0,1]，故直观看上去产生强烈震荡，实际上只是在低准确率处小幅震荡，同样欠拟合。
   2. 使用SGD Momentum优化算法时，可以看到损失函数在大幅下降后存在震荡情况，收敛并不平滑，这也许是由动量衰减因素引起的。此时，测试集正确率能达到39.72%，为该Softmax分类器的最优训练结果，但从测试机正确率图像可以看出，测试机正确率的上涨幅度极小，几乎是一条平稳的直线。

最终选用的最优优化算法及其参数为：SGD算法，学习率0.03，动量衰减因数0.9，权重衰减1e-5

torch.optim.SGD(net.parameters(),lr=0.03,momentum=0.9, weight_decay=1e-5) 

综上所述，Softmax线性分类器对CIFAR10数据集的分类效果较差，模型训练的拟合效果较差，这是由于，单层神经网络的线性分类器与多维的图像本就难以拟合，为了转换为二维的矩阵计算，将图像的数据进行平展，损失了图像的空间结构信息。

2）MLP模型

通过实验，在SGD算法，学习率0.03，动量衰减因数0.9，权重衰减1e-5条件下，对比了单隐藏层与三隐藏层网络结构的训练效果。

运行结果：

网络结构	损失值	测试集表现
input hidden 1(512) output epoch=40		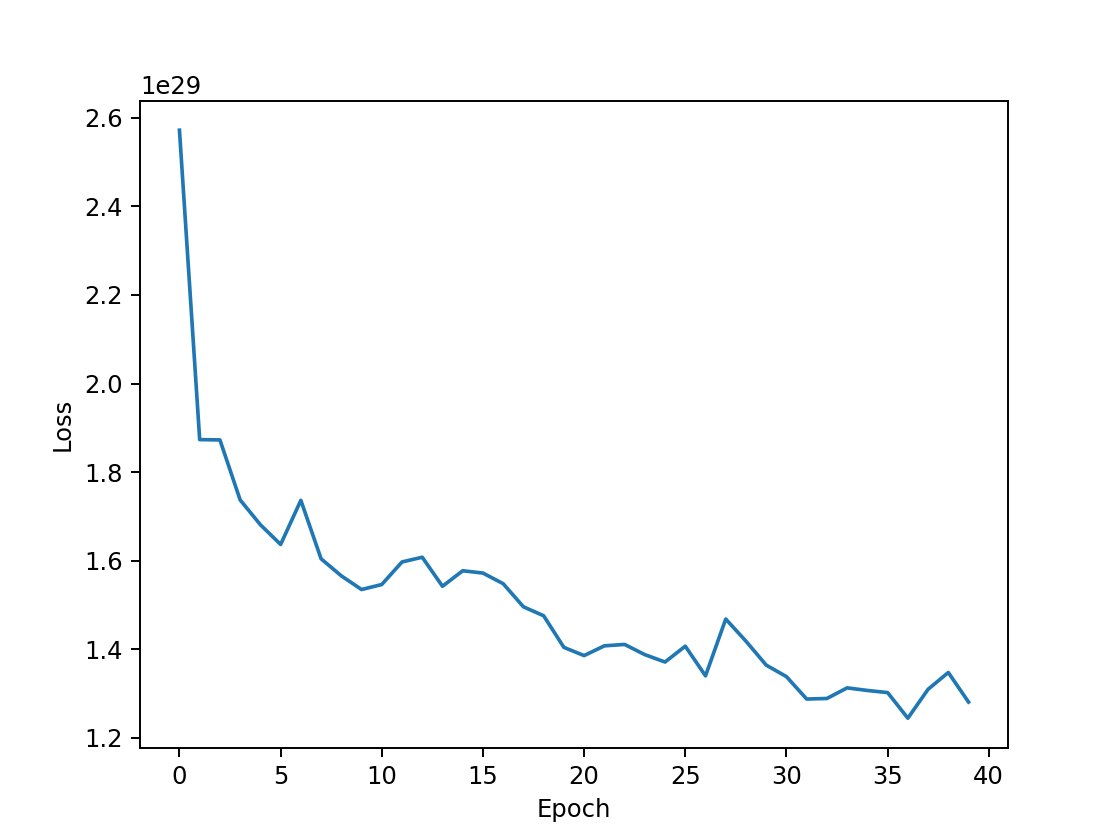50.71%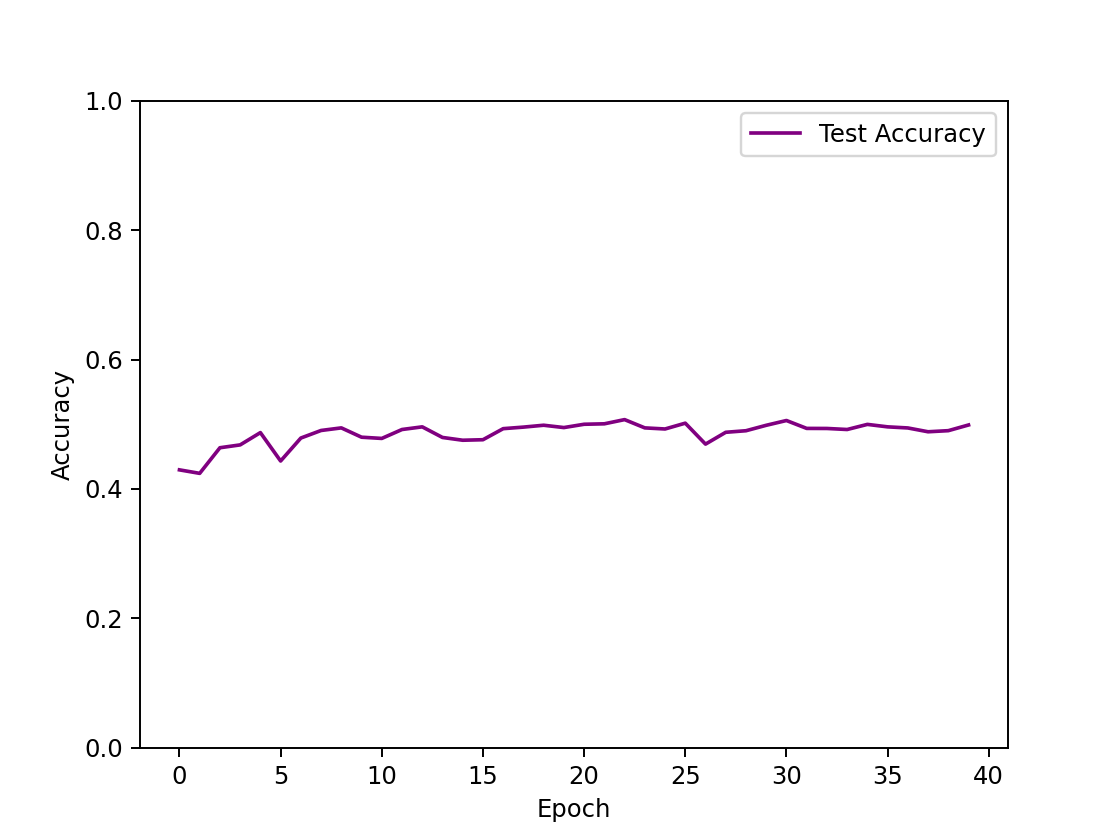
input hidden 1(120) output epoch=20		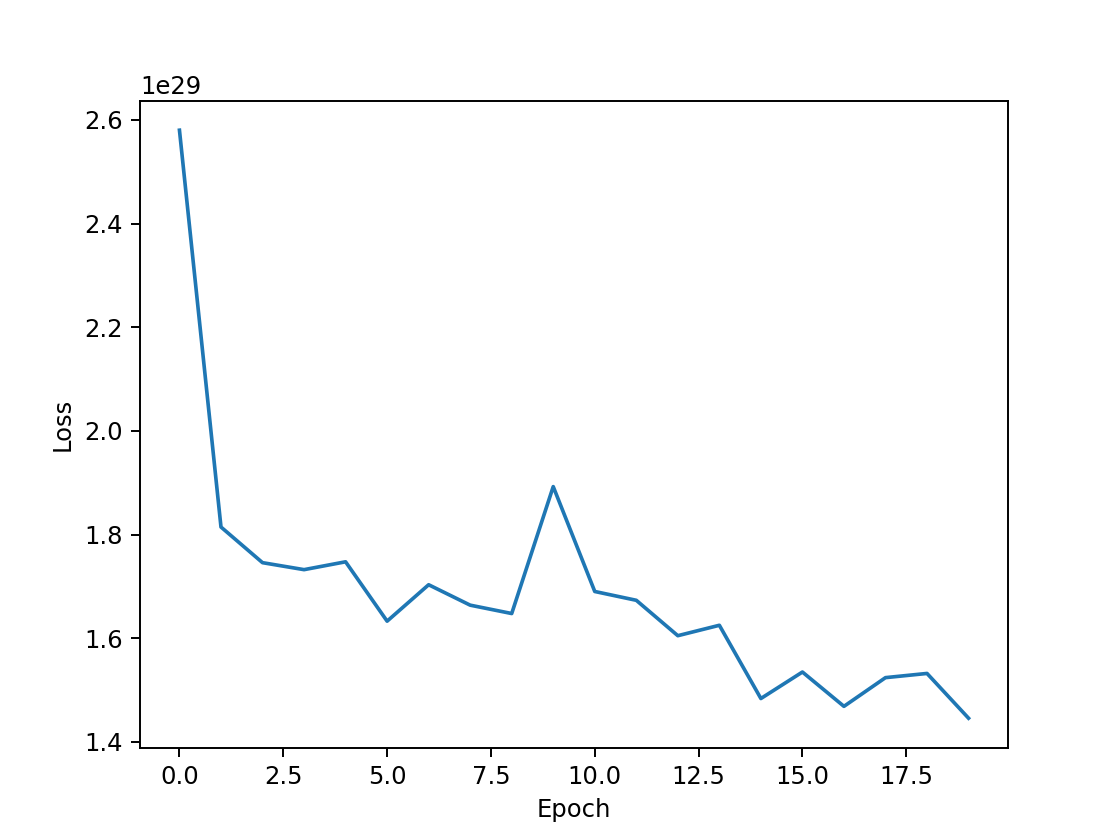49.72%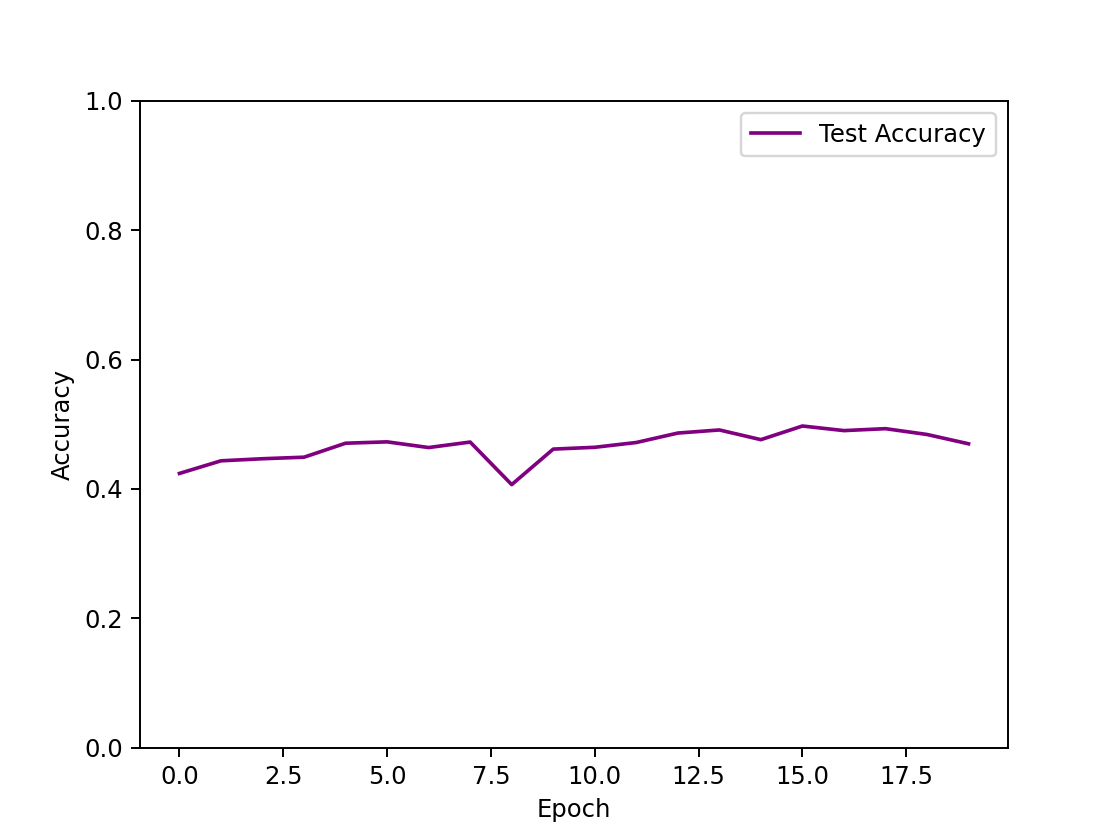
input hidden 1(1024) hidden 2 (256) hidden 3(84) out epoch=60		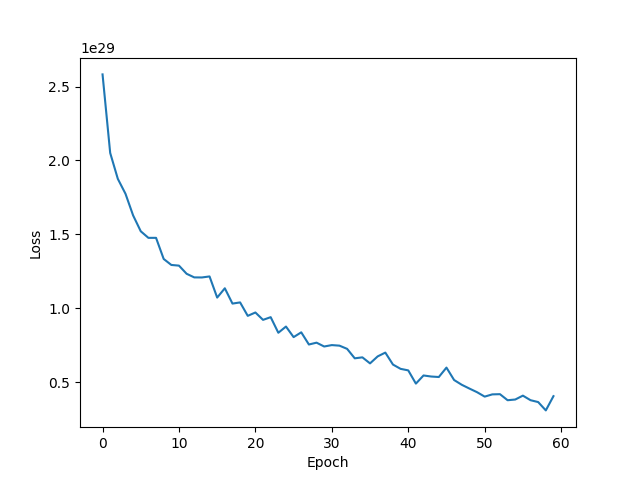58.41%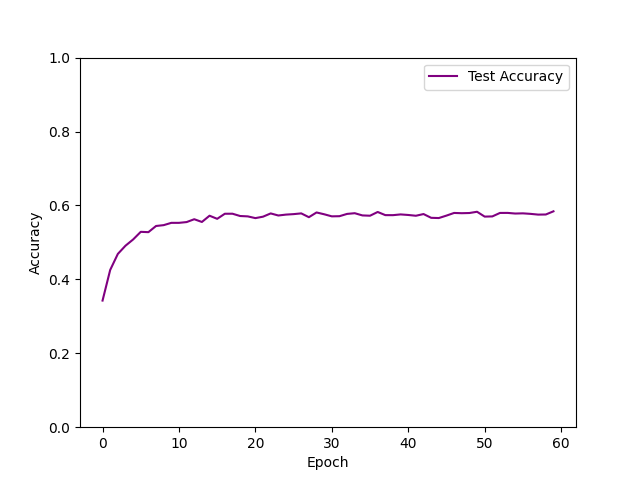
input hidden 1(4096) hidden 2 (1280) hidden 3(256) hidden4(64) out epoch=40		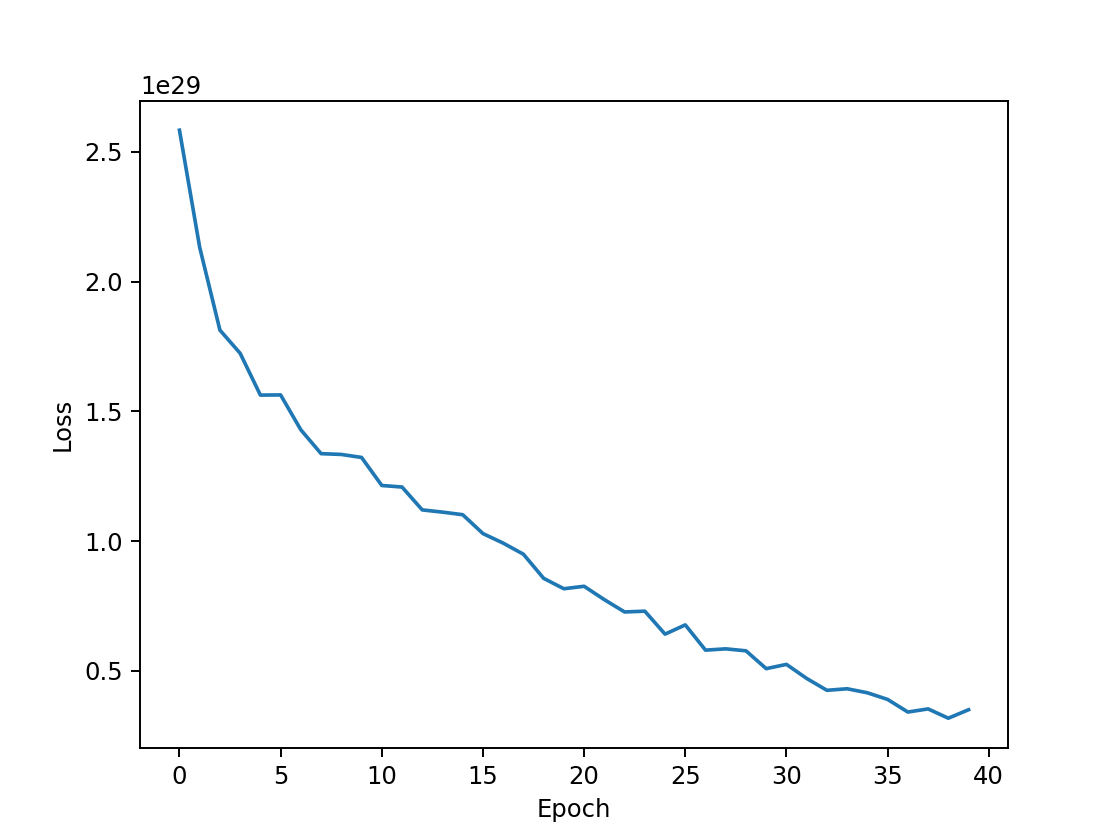60.09%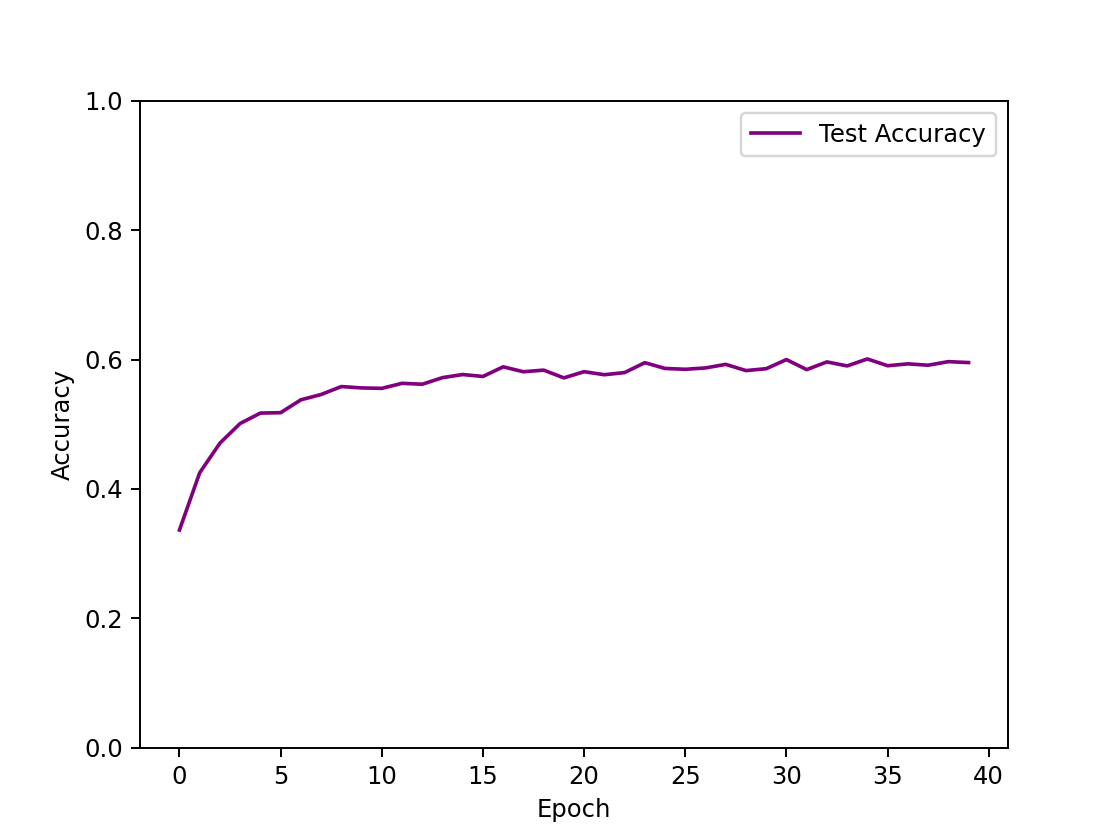

从表中可以看出：

1. 在训练效率上，网络结构对用时影响甚微，时间基本为18s/epoch。
2. 在训练效果上：
   1. 隐藏层数量的影响：隐藏层越多，非线性的比重更大，模型的拟合效果越好，预测正确率越高。对于单隐藏层的网络结构，最高正确率在50%左右，从图像可以看出，损失函数收敛不平滑，测试集正确率仅从40%上升到50%，训练效果较差，欠拟合。对多隐藏层的网络结构，正确率能接近60%左右，三隐藏层的最高正确率为58%，四隐藏层迭代次数更少而正确率更高，为60%。然而，此时损失函数皆未完全收敛，测试集正确率却已收敛不再增加，说明模型欠拟合。
   2. 隐藏层神经元数量的影响：在适当范围内，隐藏层神经元数量越多，拟合效果越好。理论上，隐藏层中使用太少的神经元将导致欠拟合(underfitting)。相反，使用过多的神经元同样会导致一些问题。首先，隐藏层中的神经元过多可能会导致过拟合(overfitting)。当神经网络具有过多的节点（过多的信息处理能力）时，训练集中包含的有限信息量不足以训练隐藏层中的所有神经元，因此就会导致过拟合。即使训练数据包含的信息量足够，隐藏层中过多的神经元会增加训练时间，从而难以达到预期的效果。

3）CNN模型

以LeNet网络结构为基础，通过实验，分别对比了优化算法及其参数、网络结构对训练效果的影响。

1、对优化算法及其参数的实验

在LeNet网络结构下，探究不同优化算法及其参数对训练性能的影响。

运行结果：

优化器及参数	损失值	测试集表现
SGD lr=0.03 momentum=0.9 weight_decay=1e-5 epoch=60		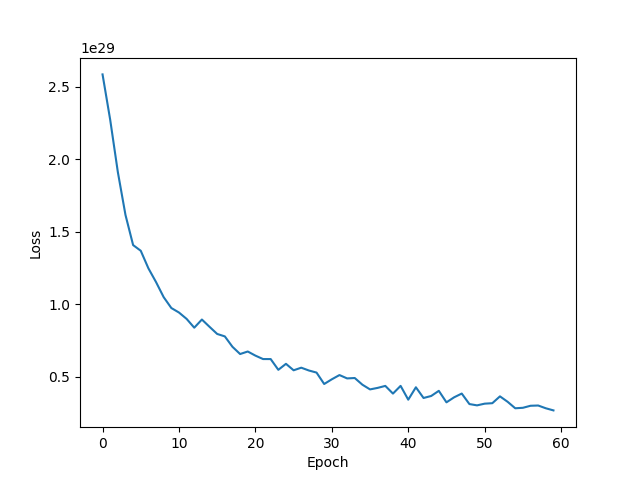73.82%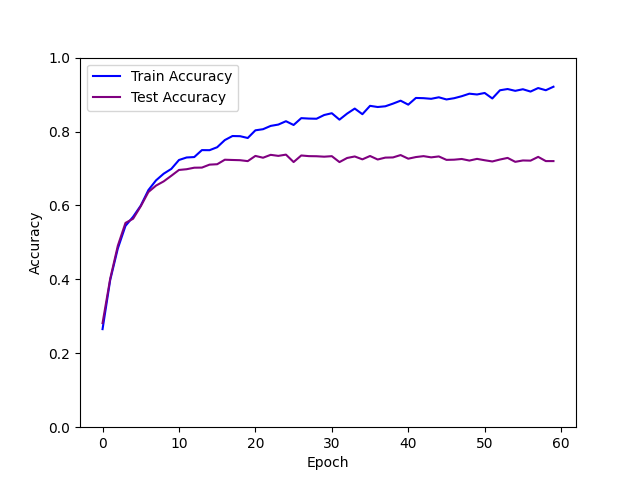
Adam lr=0.001 weight_decay=1e-5 epoch=50		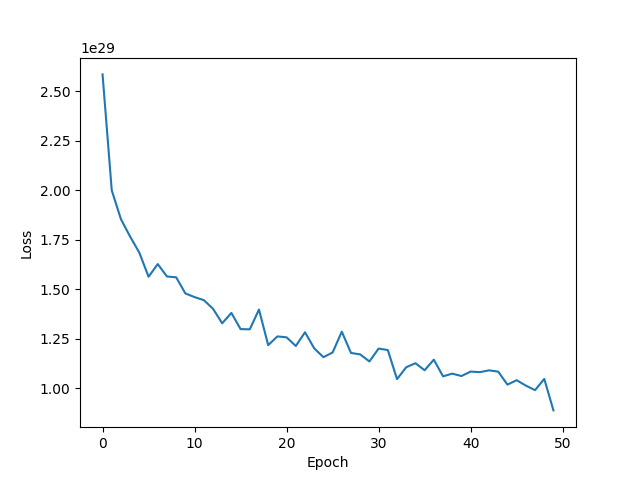62.26%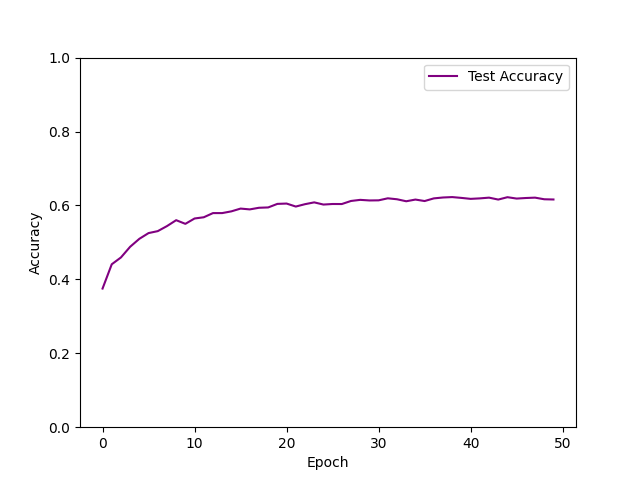
SGD lr=0.03 weight_decay=1e-5 epoch=50		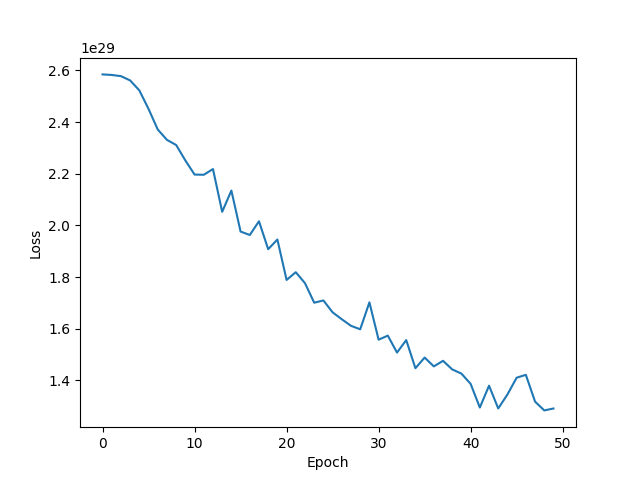61.37%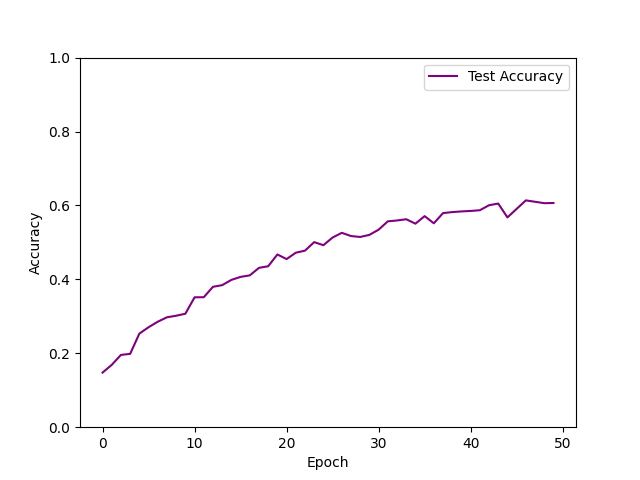

从表中可以看出，在训练效果上：

1. 使用SGD Momentum优化算法时，经过60次迭代，损失函数正常收敛；模型拟合效果最好，测试集正确率最高，能达到73.82%，训练集正确率能达到90%。
2. 使用Adam优化算法时，模型拟合效果较差，正确率仅为62%，也许是因为默认的学习率太低。
3. 使用SGD优化算法时，缺乏动量衰减因子后，损失函数收敛速度明显变慢，接近最优点的速度变慢，震荡情况增加，模型拟合效果较差，测试集正确率仅为61%。

2、对网络结构的实验

在SGD算法，学习率0.03，动量衰减因数0.9，权重衰减1e-5条件下，对不同的网络结构进行实验。

运行结果：

网络结构	测试集表现及用时
LeNet: input Conv(out_channels=6,conv_size=5) MaxPool($2\times2$) Conv(out_channels=16,conv_size=5) MaxPool($2\times2$) linear(120) linear(84) out(10)	73.82%
在LeNet基础上添加一个卷积层、一个全连接层: input Conv(out_channels=16,kern_size=5) Conv(out_channels=32,kern_size=5) MaxPool($2\times2$) Conv(out_channels=64,conv_size=5) MaxPool($2\times2$) linear(256) linear(120) linear(84) out(10)	74.5%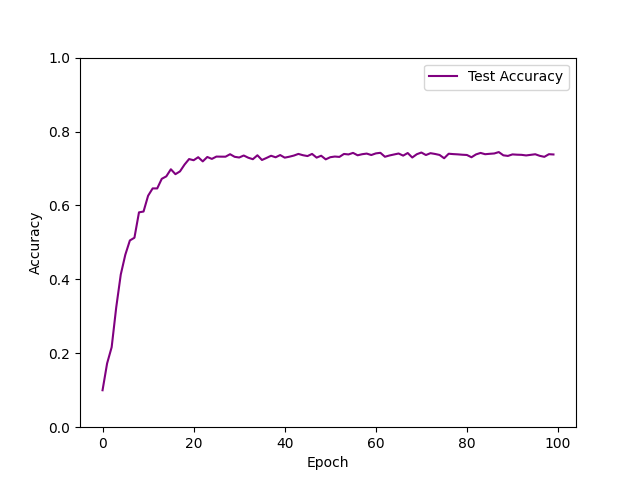
input Conv(out_channels=32,kern_size=3,pad=1) MaxPool($2\times2$) Conv(out_channels=64,kern_size=3,pad=1) MaxPool($2\times2$) linear(1024) linear(512) out(10)	77.89%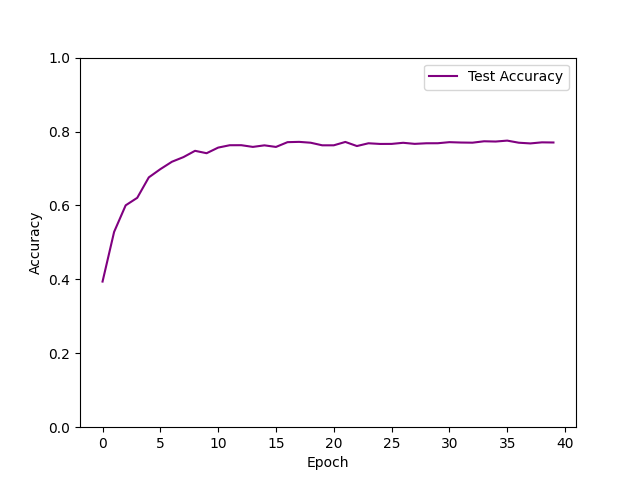
在LeNet基础上添加两个卷积层、一个全连接层: input Conv(out_channels=6,kern_size=2,pad=2) Conv(out_channels=16,kern_size=2,pad=2) MaxPool($2\times2$) Conv(out_channels=64,conv_size=2,pad=2) MaxPool($2\times2$) Conv(out_channels=128,conv_size=3,pad=2) linear(2069) linear(496) linear(84) out(10)	78.59%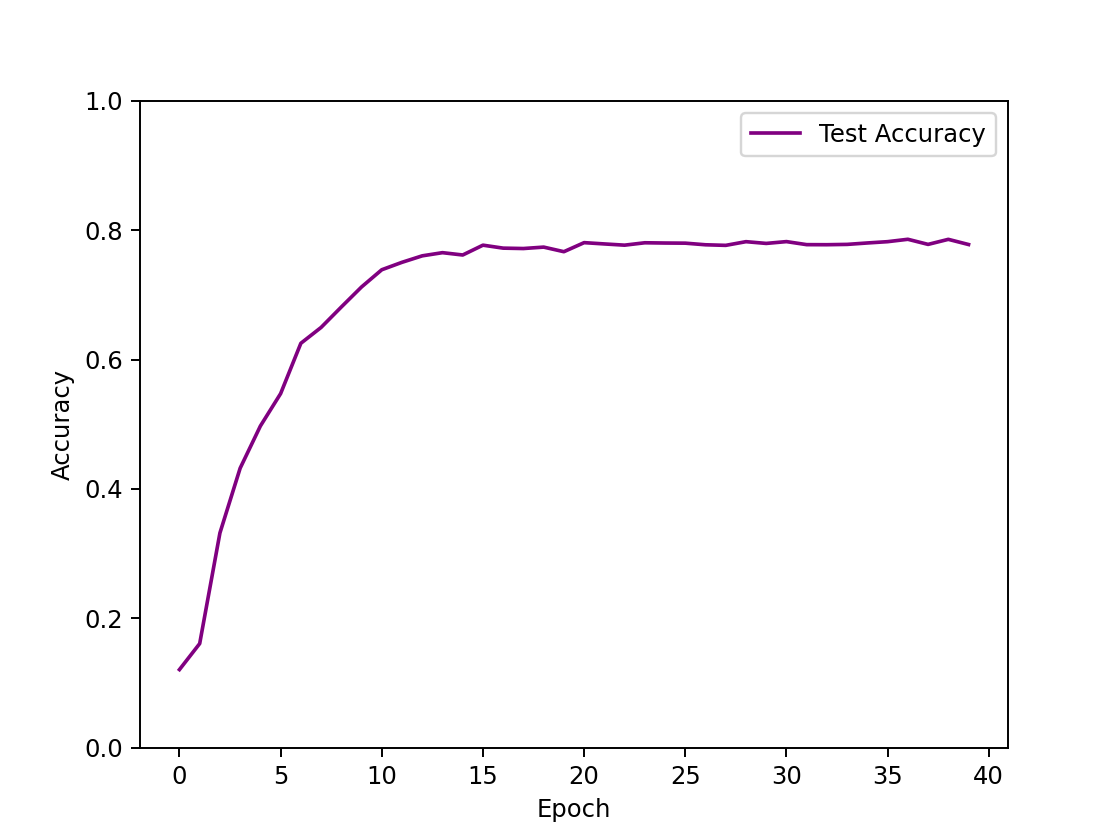

从表中可以看出：

1. 在训练效率上，相同条件下，卷积层数越少，模型收敛速度越快，且单次epoch用时越少，但网络结构含有2~4个卷积层时一般在18s/epoch左右浮动，实际变动不明显。对于只有两个卷积层、三个全连接层的CNN网络结构，只需要15 epoch就能收敛到最优的正确率。若有三个卷积层、四个全连接层，则需要30 epoch来达到收敛。若有四个卷积层，四个全连接层，用该网络结构训练了两次，epoch皆为25，此时损失函数还未收敛，仍然呈下降趋势，说明收敛速度较慢。
2. 在训练效果上：适当增加卷积层、减小卷积核大小，添加零填充层能够增强模型的拟合效果，提高正确率。在适当的范围内，卷积核越小，意味着图像的特征采样越细，故可以提高准确率。添加零填充层，可以防止对边缘像素信息的遗失。若有四个卷积层，四个全连接层，用该网络结构训练了四次，迭代到25次时，一次达到了78%的正确率且已收敛，两次则只达到56%且已收敛，说明卷积层过多，可能出现过拟合的情况。此外，用SGD Momentum优化算法，也可能导致对局部最优点的搜索具有随机性。卷积层过多时，会导致神经元失效，尝试了七层卷积层，正确率一直为0.1，正好10个分类，神经元已经陷入瞎猜。

4）对比三个模型在CIFAR-10图像分类任务上的性能

显然的，CNN模型在图像分类任务上训练效果最佳，最高测试集正确率能达到77%，远超另外两个模型，这是由于Softmax线性模型与MLP模型都基于线性计算，需要将图像的数据进行平展，损失了图像的空间结构信息，而CNN模型可以通过卷积运算，保留读取这些结构信息。次之的是MLP模型，通过增加隐藏层数量，可以得到非线性模型的训练效果，最高测试集正确率能达到60%。拟合效果最差的则是Softmax模型，单层神经网络的线性分类器与多维的图像本就难以拟合，并非意外结果。

在训练效率上，事实上，无论是基于优化算法的实验，还是网络结构的实验，或是模型的实验，都较难观察出训练速度的差别，基本在18s/epoch左右。我在本实验中采用了GPU加速，但对于该模型，BatchSize=500时，极少数情况下，N卡占用率才能达到70%，多数时间有大量空余，真正占用时间的是迭代数据时，CPU对数据集图像的读取及预处理（即transform操作），而非与优化算法、网络机构、模型有关的计算，这是由于用dataloader读取数据时，每epoch要对数据做一次预处理、转换为张量的操作，再迭代取数据，CPU对Tensor的处理很慢，而torchvision库没有将数据集迁移到GPU进行预处理计算的API。因此，未能观察出训练速度的差别。若要解决这个问题，只能使用DALI或其余库接口加速预处理与数据读取，或者将预处理后的数据集进行保存。