用变邻域搜索、模拟退火、遗传算法解决TSP问题
完整代码见该项目仓库
1. 算法原理
模拟退火算法与遗传算法皆为在局部搜索基础上的优化算法。局部搜索(Local Search)是指寻找近似最优解、不断优化局部最优解的启发式算法。其基本思路为,算法从一个或若干个初始解出发,在当前状态的邻域中搜索出若干个候选解,并以某种策略在候选解中确定新的当前解;重复执行上述搜索过程,直至满足算法终止条件,结束搜索过程并输出近似最优结果。
1、获取新邻域的算子设计
无论是变邻域算法与模拟退火算法的扰动操作、变邻域操作,还是遗传算法的变异操作,本质上都是产生新邻域的随机解,都可采用以下算子。
1)将路径四个区间随机排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#扰动产生新的随机解,扰动方式为分成四个区间随机排序
def shaking(path):
global size
ini = visited[path]
cnt = 0
while True:
pos1,pos2,pos3 = sorted(random.sample(range(0,size),3))
path_ = path[pos1:pos2] + path[:pos1] + path[pos3:] + path[pos2:pos3]
if path_ not in visited:
cost = getCost(path_)
visited.update({path_:cost})
else:
cost = visited[path_]
cnt+=1
if ini >= cost:
break
elif cnt > 100:
path_ = path
cost = ini
break
return path_
2)反转一段区间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#反转一段区间,获取新邻域
def getNei_rev(path):
global size
min = visited[path]
cnt = 0
while True:
i,j = sorted(random.sample(range(1,size-1),2))
path_ = path[:i] + path[i:j+1][::-1] + path[j+1:]
if path_ not in visited:
cost = getCost(path_)
visited.update({path_:cost})
else:
cost = visited[path_]
cnt+=1
if cost < min:
min = cost
break
elif cnt > 1000:
path_ = path
break
return path_,min
3)交换两个城市
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#交换两个城市,获取新邻域
def getNei_exc(path):
global size
min = visited[path]
cnt = 0
while True:
i,j = sorted(random.sample(range(1,size-1),2))
path_ = path[:i] + path[j:j+1] + path[i+1:j] + path[i:i+1] + path[j+1:]
if path_ not in visited:
cost = getCost(path_)
visited.update({path_:cost})
else:
cost = visited[path_]
cnt+=1
if cost < min:
min = cost
break
elif cnt > 1000:
path_ = path
break
return path_,min
4)随机挑选两个城市插入序列头部
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#随机挑选两个城市插入序列头部,获取新邻域
def getNei_ins(path):
global size
min = visited[path]
cnt = 0
while True:
i,j = sorted(random.sample(range(1,size-1),2))
path_ = path[i:i+1] + path[j:j+1] + path[:i] + path[i+1:j] + path[j+1:]
if path_ not in visited:
cost = getCost(path_)
visited.update({path_:cost})
else:
cost = visited[path_]
cnt+=1
if cost < min:
min = cost
break
elif cnt > 1000:
path_ = path
break
return path_,min
2、变邻域搜索算法(VNS)
变邻域搜索算法(Variable Neighborhood Search)是一种改进的局部搜索算法。此处的邻域,是指当前状态的临近状态,通过扰动、变邻域等函数操作,在邻域中产生新的随机解,选择其中的局部优解替代当前解,反复迭代,以此逼近最优解。
VNS的算法思路为:
- 初始化,选择一个可行的初始解;
- 扰动当前解,获得一个新的解;
- 使用变邻域(Variable Neighborhood Descent, VND)策略的局部搜索:
- 用当前解作为初始解
- 对当前解做变邻域操作,假如得到的解比当前解更优,将变邻域后得到的解作为下一次迭代的当前解
- 重复第二步,直到迭代次数满足终止条件,返回局部最优解,退出迭代
- 假如在VND操作中获得的局部最优解较当前解更优,则令其替代当前解,将迭代计数置为0;反之,迭代计数加一。
- 返回第二步,重复直到迭代次数满足终止条件,返回近似最优解,退出迭代。
其伪代码为:
VNS:

VND策略:

3、模拟退火(SA)
基于上述的变邻域搜索算法,加入模拟退火策略,即为模拟退火算法。
模拟退火算法的原理类似固体的物理退火过程,在进行随机生成解的过程中,接受劣解的概率逐渐下降趋近0,由随机搜索(高温)转变为局部搜索(降温),最终算法找到最优解(达到物理基态)。
模拟退火算法的本质是通过温度来控制算法接受劣解的概率。
退火系数在0.99,\(\frac{1}{lg(k+1)}\)(经典退火),\(\frac{1}{k+1}\)(快速退火)三者之间选择,其中最后一个系数搜索效率较快。
接受劣解的概率公式为:\(e^{\frac{f(x)-f(x')}{tk}}\)
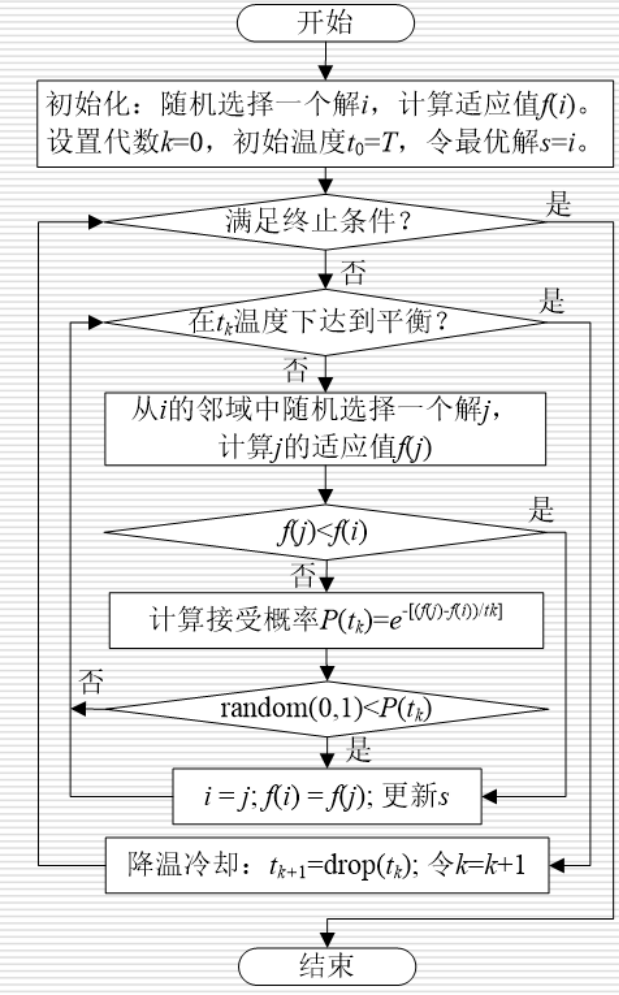
SA的算法思路为:
- 初始化,选择一个可行的初始解,以路径总长度为适应值,长度越短,解越优,越适应环境;
- 在当前解的邻域中随机选择一个解,若该解优于当前解,替换该解为当前解;反之,计算接受概率,若产生的介于(0,1)之间的随即小数小于该概率,则接受该劣解,否则以当前解继续下一次迭代。
- 重复第二步,直到搜索在当前温度下达到收敛,进行降温冷却操作,返回第二步;
- 重复二、三步直到温度降温至满足终止条件,返回近似最优解,退出迭代。
其伪代码为:
4、遗传算法(GA)
遗传算法的基本原理是通过作用于染色体上的基因寻找好的染色体来求解问题,它需要对算法所产生的每个染色体进行评价,并基于适应度值来选择染色体,使适应性好的染色体有更多的繁殖机会,在遗传算法中,通过随机方式产生若干个所求解问题的数字编码,即染色体,形成初始种群;通过适应度函数给每个个体一个数值评价,淘汰低适应度的个体,选择高适应度的个体参加遗传操作,经过遗传操作后的个体集合形成下一代新的种群,对这个新的种群进行下一轮的进化。
遗传算法主要分为四个部分:交叉(crossover)、变异(mutation)、评估(fitness)、选择(selection)。
交叉算子有:部分映射(Partial-Mapped Crossover)、顺序交叉(OX crossover)、基于位置的交叉(Position-based Crossover )、基于顺序的交叉(Order-Based Crossover )、循环交叉(Cycle Crossover)。在本实验中采取部分映射法(PMX)。
变异算子有:反转变异(Invertion)、插入变异(Insertion)、替代变异(displacement)、交换变异(swap)、启发式变异(heuristic)。在本实验中测试反转变异与交换变异,结果表明反转变异的效率要优于交换变异。
GA的算法思路为:
- 初始化,选择一个可行的初始解种群,对该种群的适应度进行评估;
- 对当前解种群进行交叉、变异、评估操作;
- 在当前解与经过交叉变异得到的子种群中,根据适应度评估值进行选择,得到下一代种群,重复第二步;
- 重复二、三步直到迭代次数满足终止条件,返回近似最优解,退出迭代。
其伪代码为:

2. 关键代码展示
1、读取输入,存储地图
读取城市的横纵坐标后,求出两两间的二维欧几里得距离,用一个全局变量DIST二维数组进行记录,使计算路径长度时无需反复计算两城市间的二维欧几里得距离。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#读取城市的x,y坐标
def load(txt):
f = open(txt)
map=[]
flag = 0
for line in f:
line = line.strip()
if line == "NODE_COORD_SECTION":
flag = 1
continue
if line == "EOF":
break
if flag:
a = line.split()
map.append((float(a[1]),float(a[2])))
return tuple(map)
#获取两个城市间的二维欧几里得距离
def getDist():
global map,size
dist = np.zeros((size,size))
for i in range(0,size):
for j in range(0,size):
dist[i][j] = ((map[i][0]-map[j][0])**2 + (map[i][1]-map[j][1])**2)**0.5
return dist
2、计算路径长度
1
2
3
4
5
6
7
8
9
#根据路径获取该路径总代价
def getCost(path):
cost = 0
former = path[0]
for city in path:
cost += DIST[former][city]
former = city
cost += DIST[path[0]][path[-1]]
return cost
3、VND
在局部搜索中使用VND策略进行搜索。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#在Local Search中使用VND方法进行搜索
def VND(path):
l = 0
min = visited[path]
while l < 3:
if l == 0:
path_,cost = getNei_rev(path)
elif l == 1:
path_,cost = getNei_exc(path)
elif l == 2:
path_,cost = getNei_ins(path)
if cost < min:
path = path_
min = cost
l = 0
else:
l+=1
return path,min
4、VNS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#进行变邻域局部搜素
def VNS(path,kmax):
k = 0
temp = path
min = solutions[0]
global count
while k < kmax:
#扰动后进行变邻域操作
path_nei,cost = VND(shaking(temp))
print(cost)
solutions.append(cost)
count+=1
if cost < min:
temp = path_nei #记录迭代过的最优的解
min = cost
k = 0
else:
k+=1
return temp,min
5、SA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#模拟退火算法
def SA(path,kmax,t0,t_end):
temp = path
min = solutions[0]
result = [temp,min] #记录迭代过的最优的解
global count
t = t0 #初始温度
while t > t_end:
for k in range(1,kmax):
path_nei,cost = VND(temp) #进行变邻域操作
#print(cost)
solutions.append(cost)
count+=1
#判断是否接受该解
if cost < min or random.random() < np.exp(-((cost-min)/t*k)):
temp = path_nei
min = cost
if cost < result[1]:
result = [path_nei,cost]
#t/=math.log10(1+k)
t/=k+1 #降温操作
return result[0],result[1]
6、PMX
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#Partial-Mapped crossover
def PMX(i,j):
global size
s,t = sorted(random.sample(range(1,size),2))
next_i = list(i[:s] + j[s:t] + i[t:])
next_j = list(j[:s] + i[s:t] + j[t:])
#建立映射表
mapped_i = {next_i[k]:next_j[k] for k in range(s,t)}
mapped_j = {next_j[k]:next_i[k] for k in range(s,t)}
#判断是否满足解的条件(每个城市皆访问一次)
while len(set(next_i)) != len(next_i):
for k in range(size):
if k < t and k >= s:
continue
while next_i[k] in j[s:t]:
next_i[k] = mapped_i[next_i[k]]
while len(set(next_j)) != len(next_j):
for k in range(size):
if k < t and k >= s:
continue
while next_j[k] in i[s:t]:
next_j[k] = mapped_j[next_j[k]]
next_i = tuple(next_i)
next_j = tuple(next_j)
if next_i not in visited:
visited.update({next_i:getCost(next_i)})
if next_j not in visited:
visited.update({next_j:getCost(next_j)})
return next_i,next_j
7、GA
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#遗传算法
def GA(paths,kmax):
global M,solutions
temp = paths
for k in range(kmax):
count = 0
flag = 0
children = [] #存储此代交叉、变异产生的子种群
#加入当前种群中的最优解,使得下一代种群的最优解一定不会劣于当前种群最优解
children.append(temp[0])
for l in range(M):
while True:
i,j = random.sample(range(M),2)
count+=1
if temp[i] != temp[j]:
break
if count > 1000000:
flag = 1
break
if flag == 0:
a,b = PMX(temp[i],temp[j]) #使用PMX交叉操作
children.append(a)
children.append(b)
for l in range(M):
i = random.randrange(M)
children.append(reverse(temp[i])) #使用反转一段区间作为变异操作
temp = sorted(children[:], key=lambda x:visited[x])[:M] #选取子代中最优的前M个解
solutions.append(visited[temp[0]]) #记录此次迭代产生的下一代的最优解
print(k,visited[temp[0]])
return temp[0]
3. 创新点与优化
1、缩短迭代中计算距离的时间
1)用一个全局变量DIST二维数组记录所有城市两两间的距离,使计算路径长度时无需反复计算两城市间的二维欧几里得距离。
2)用一个全局变量visited字典记录已经搜索过的路径,以元组储存路径作为键值,储存其路径长度。在搜索过程中,可能多次搜索到同一条路径,可以在visited字典中直接获取路径,无需反复计算。
2、控制搜索方向向最优化迭代
1)在扰动、变邻域、变异操作中,通过反复随机生成路径,选择候选解中优于当前解的路径;若多次随机后当前路径仍然为最优,则返回此次已搜索路径中的最优解。通过控制最大随机生成路径的次数,可以有效控制搜索方向向最优化迭代,效率提高。
2)在遗传算法中,每一次迭代,将当代种群的最优路径复制到子代种群,在经过交叉、变异操作后,使用精英(elitist)策略,再在子代种群中选择最优的前M(种群大小)个解,以此保证下一代种群的最优解一定不会劣于当前种群最优解,搜索方向向最优化迭代。